国家粮食和物资储备局科学研究院

分享到：

小麦竖向通风阻力研究

发布时间：2016-08-11

尹君石天玉魏雷赵会义张洪清刘杰李锦王芳

竖向通风是目前粮仓最常用的通风形式，分为上行压入式和下行吸出式两种，对实仓条件下竖向通风粮堆阻力的测试研究较少，张来林（1993）、杨进（2001）、和杨英强（2008）分别采用了200～300mm直径的料筒做了一些粮种的上行压入式竖向通风试验，探讨了不同粮种在上行压入式通风时粮堆阻力的变化情况。由于这些单向通风试验模拟所用的料筒直径较小，与大截面的实仓条件有一定的差别。本研究利用180t仓容的平房仓式中试仓对上行压入式和下行吸出式竖向通风时小麦粮堆的阻力特性进行研究，掌握不同通风方向的粮堆阻力的变化规律，从而为发展储粮竖向通风技术提供理论支撑。

1. 材料和方法

1.1 试验仓

国家粮食局科学研究院粮食储运国家工程实验室中试平台，1个180t仓容的大型双层全钢结构仓房，仓房内部净尺寸为长8.8m，宽4.2m，高7.7m，粮食堆高5.7m。

仓房底面为一块桥式冲孔板，冲孔板下面为一夹层空间，夹层底板上有通风口。通风气流可以从通风口流入或流出夹层空间。通风口与风机进口或出口连接，实现竖向通风时上行压入式和下行吸出式通风。下行吸出式通风系统如图1所示，上行压入式通风时气流方向与图示方向相反。

1.2 试验材料

1.2.1 供试粮食

试验粮种为小麦，基本情况如表1。

1.2.2 通风设备

变频调速风机，型号Y160M2－2，额定风量16000m³/h，额定风压2940Pa，额定功率15kW。与仓房底部风口采用PVC硬管连接。风机进出口连接管内径480mm。

1.2.3 测试仪器

通风测试仪器如表2，其中埋入式毕托管布置到粮堆内部和空间的各测试点位置。

1.3 试验方法

1.3.1 总风量和总阻力检测

在仓外风机出口的直管段A处（见图1）沿水平和垂直方向各开1个测孔，在该截面采用等面积分环法共设16个测点，用风速仪和毕托管测量A截面各点的风速、全压和静压，计算不同工况时的通风量。

1.3.2 粮堆内静压检测

向仓内边装小麦边布置毕托管，在粮堆1000mm和4000mm的高度布置两层，每层4行9列共布置36个测点，两层共72个测点，各测点位置如图2所示。毕托管再用硅胶管道连接，将硅胶管道引到粮堆表面的密封薄膜外，所有的毕托管布置好后。粮堆表面用PA/PE五层共挤尼龙薄膜压入气调专用槽管，形成单面密封。密封后检测气密性，-300Pa到-150Pa的半衰期为180s。

1.3.3 粮面以上空间和底面以下空间的测试点布置

在距粮面以上500mm的空间水平面安装5个测点，仓房底部夹层空间距离粮仓底面500mm处安装5个测点。各测点位置如图3所示。

1.3.4 参数测定与计算

把通风机进口与仓房东侧主风道出口相连接，开启通风机，使环境大气从仓顶通风口吸入垂直向下穿过粮堆从底部风道排出，而后经过通风机排入大气，进行下行吸出式通风；通风机电机的频率分别调到40、35、30、25、20、15和10Hz，每个频率下风机运行稳定后，分别采用表2中的测试仪器测量系统总风量和1m及4m粮层的平均静压值。

当各种工况测试完毕后，把通风机出口与仓房东侧主风道出口相连接，使环境大气经过通风机后从仓底通风口压入并垂直向上穿过粮堆从顶部风口排出，进行上行压入式通风。通风机电机的频率分别调到35、30、25、20、15和10Hz，每个频率下风机运行稳定后，分别采用表2中的测试仪器测量系统总风量和1m及4m粮层的平均静压值。

1.3.5 系统总风量测定与计算

利用等面积分环法，采用手持式智能风速仪测定风机出口A截面各点的风速，并换算成截面平均值：

式中：Q—所测量截面平均风量，m³/h；v—所测量截面上各测点的风速，m/s；V—平均风速，m/s；S—测试截面的流通面积，m²；Hd—所测量截面平均动压，Pa；ρ—空气密度，kg/m³；n—截面上的测点数。

1.3.6 粮堆阻力测定与计算

用埋入式毕托管和手持式数字压力仪测定粮堆距冲孔底板1m和4m两截面各点的平均静压Z1和Z4，从而计算以下参数：

（1）单位粮层阻力：Z_m=｜Z₄-Z₁｜/3

式中:Z_m—单位粮层阻力（为粮堆内1m和4m两截面平均静压差除以两截面间距）,Pa/m；Z₁—距离冲孔底板上1m截面上的平均静压，Pa；Z₄—距离冲孔底板上4m截面上的平均静压，Pa

（2）距离冲孔底板1m以上粮堆的内部粮层阻力：Z_z/Pa=5×Z_m

1.3.7 粮堆表观风速和单位通风量计算

粮堆表观风速/（m³/s/m²）=系统总风量除以与气流垂直方向的粮堆截面积

单位通风量/（m³/h/t）=系统总风量除以粮堆总重量

2. 结果与分析

2.1 不同表观风速下的粮堆阻力

粮堆不同表观风速下下行吸出式竖向通风试验中（见表3），粮堆内表观风速由0.0066m/s增加到0.0656m/s，对应的单位通风量由5.54m³/h/t增加到55.22m³/h/t，小麦粮堆单位粮层阻力由11.4Pa/m增加到85.0Pa/m。说明表观风速和单位通风量增加，粮堆的单位粮层阻力也增加，两者呈正相关。

粮堆不同表观风速下上行压入式竖向通风试验中（见表4），粮堆内表观风速由0.0066m/s增加到0.0411m/s，对应的单位通风量由5.6m³/h/t增加到34.6m³/h/t，小麦粮堆单位粮层阻力由10.0Pa/m增加到63.3Pa/m。说明压入式竖向通风的表观风速和单位通风量增加，粮堆的单位粮层阻力也增加，两者呈正相关。

2.2 粮堆表观风速与粮堆表层阻力

根据表3和表4的数据，计算单位粮层阻力Z_m，单位粮层阻力Z_m乘以4.7计算出4.7m小麦粮堆粮层阻力Z_z。但是通过实测得到的上层4.7m粮堆的阻力Z1与按照单位粮层阻力计算得到的上层4.7m粮堆阻力Z_z相比，Z_z明显小于Z₁，且表观风速越大差值越明显。如果把整个粮堆内部单位粮层阻力视为相同，说明从粮堆空间进入或流出粮堆的空气在表层就受到一定的阻力，即Z₁与Z_z的差值，定义为粮堆表层阻力Z_b。小麦粮堆表层阻力Z_b略小于单位厚度的内部粮层阻力Z_m，Z_b与表观风速和单位通风量呈正相关，但与粮堆高度无关。在实用单位通风量范围内，吸出和压入式小麦粮堆表层阻力与粮堆表观风速的关系见图4和图5。

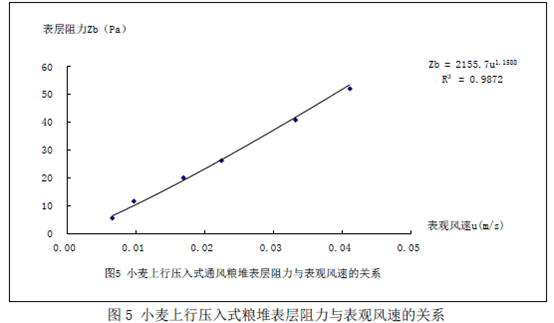
由图4和图5得到小麦下行吸出式和上行压入式通风时，用幂函数公式表示的粮堆表层阻力与表观风速的试验公式：

式中：a，b—与粮食品种和通风方向有关的系数，见表5。

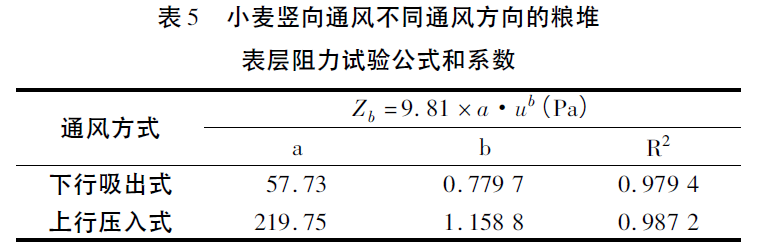
从表5可知，试验得到的幂函数公式与Shedd1953公式形式相同，说明小麦粮堆的单位粮层阻力符合多孔介质的力学规律，幂函数公式的精度可以满足工程需要。

表5中表观风速范围内，小麦上行压入式通风的表层阻力公式除以下行吸出式通风的阻力公式可以得到：

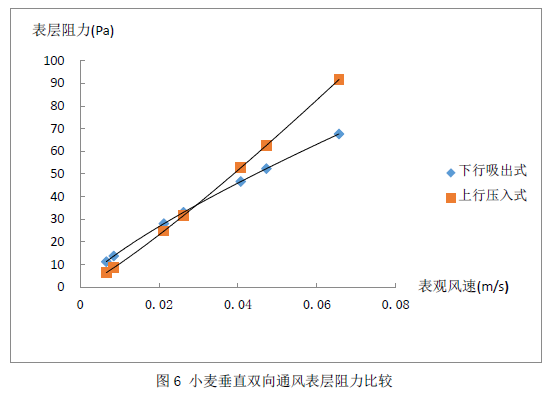
小麦粮堆在下行吸出式和上行压入式通风时的粮堆表层阻力随风量的变化规律如图6所示。当表观风速较小时，上行压入式的表层阻力小于下行吸出式的阻力；当表观风速较大时，上行压入式的表层阻力大于下行吸出式的阻力。其转折点的表观风速为0.0294m/s。

2.3 粮堆表观风速与粮堆内部单位粮层阻力

由表3和表4测定得到不同粮堆表观风速下小麦吸出式和压入式通风单位粮层阻力曲线见图7和图8：

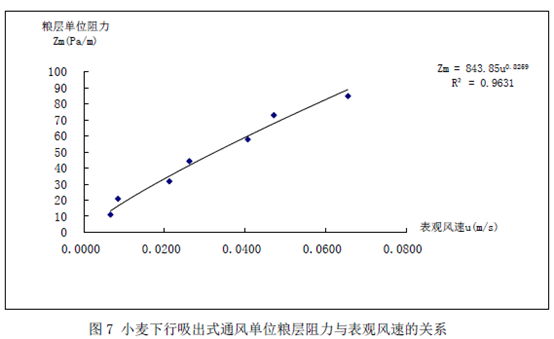
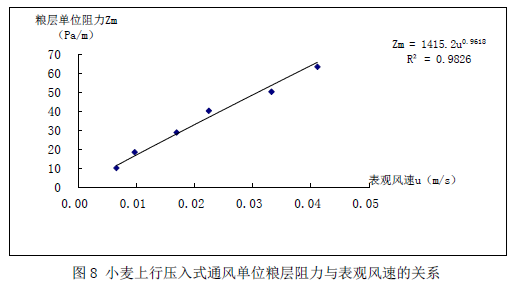
由图7和图8可知，小麦吸出式和压入式竖向通风单位粮层阻力与表观风速的关系可以用幂函数公式表示，简化成工程用经验公式为：

吸出式竖向通风（R²=0.9631）：

式中：a，b—与粮食品种和通风方向有关的系数，见表6。

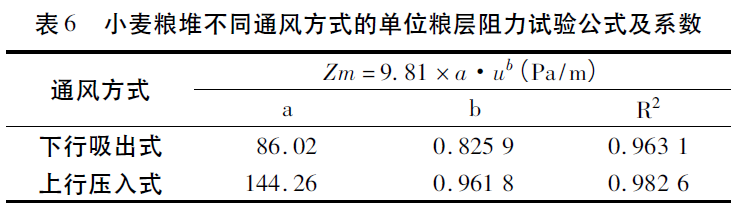
根据表6可知，试验得到的幂函数公式与Shedd公式形式相同，说明小麦粮堆的单位粮层阻力符合多孔介质的力学规律，幂函数公式的精度可以满足工程需要。

在表6所示的表观风速范围内，将小麦上行压入式通风的单位粮层阻力公式除以下行吸出式通风的阻力公式可得：

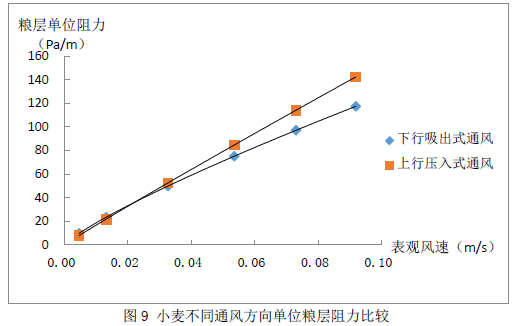
根据图9可知，当表观风速较小时，上行压入式通风的单位粮层阻力小于下行吸出式的阻力，二者非常接近；当表观风速较大时，上行压入式的单位粮层阻力大于下行吸出式的阻力，二者相差较大。转折点的表观风速为0.022m/s。

2.4 竖向通风粮堆总阻力的计算方法

由于竖向通风时粮堆表层存在附加阻力且与粮层高度无关，而内部粮层阻力与粮层高度呈正比。因此，包括表层阻力在内的粮堆总阻力并不与粮堆高度呈正比，计算粮堆总阻力的合理方法应该是粮堆内部阻力加表层阻力，即：

式中：H_粮堆—通风时粮堆总阻力，Pa；Z_b—通风时粮堆的表层阻力，Pa，按表5计算；Z_m—通风时粮堆的单位粮层阻力，Pa/m，按表6计算；H—通风方向粮堆的总高度，m。

3. 结论

小麦粮堆存在明显的表层附加阻力，定义为粮堆表层阻力，粮堆表层阻力与粮堆高度无关，可以用Shedd形式的幂函数公式（3）近似描述计算，且精度可以满足工程需要，见表5。

小麦粮堆的单位粮层阻力可以用Shedd形式的幂函数公式（6）近似描述计算，且精度可以满足工程需要，见表6。

粮堆阻力为表层阻力与内部粮层阻力之和，由于粮层阻力与粮堆高度成正比，而粮堆表层阻力与粮堆高度无关，因此粮堆总阻力并不与粮堆高度呈严格的正比关系，而应由公式（7）所确定的粮堆内部粮层阻力与表层阻力两部分之和进行计算。

小麦上行压入式通风的粮堆表层阻力和单位粮层阻力在表观风速较小时都小于下行吸出式通风，但在表观风速较大时都大于下行吸出式通风，风速越大差别越明显。由于通风阻力在不同方向通风时存在明显的差异性，说明小麦粮堆不是各向同性而是各向异性的，在储粮粮堆传热传质问题时应考虑各向异性的影响。