潘钰 张中涛 王远成 赵会义 石天玉 魏雷 

粮食储藏过程中，水分和温度是特别重要的两个参数。环境温度的季节性变化，会导致粮堆内热量传递和水分迁移，继而引起粮堆局部的温度和水分的升高，从而导致微生物和害虫的生长，使得粮仓中的粮食变得不安全。同时，粮食作为一种生命体，具有吸湿和解吸湿的特点，并且表现有呼吸作用。因此，粮堆的温度和水分变化是由粮仓外的环境和粮仓内谷物的生物特征共同决定的。

粮堆的呼吸作用会消耗粮食的干物质，同时，呼吸过程会产生热量和水分，如果粮堆通风情况不好，呼吸产生的热量和水分很难散发出去的话，就会使粮堆的水分含量不断增加，有可能引起粮堆的“出汗”甚至“结顶”。呼吸作用产生的大量热量积聚于粮堆中，如果这些热量不能及时散发出去，将会使粮温升高，有可能导致粮堆发热，甚至霉变。由此可见，粮食的呼吸作用会引起粮堆的水分和温度的变化，进而会导致粮食重量的损失、粮堆中昆虫的繁殖、粮堆的结顶、发霉等。这些情况的发生都对粮食的安全储存有直接影响。因此，粮食的呼吸作用在粮食的水分和温度变化的数值模拟中是不得不考虑的重要因素。

目前，国内学者对于“人工干预状态”（如通风等）的情况研究较多，而缺乏对“非人工干预状态”（如密闭粮仓非通风）下的探索，且国内外对于粮食的呼吸作用的研究也刚刚起步，而且研究时多假设壁温为定值，本研究考虑呼吸作用的密闭粮仓内部热湿耦合传递规律的数值模拟研究，与此前学者研究不同的是，本研究选择了逐日变化的温度作为边界条件。

1 数值模拟

1.1 物理模型

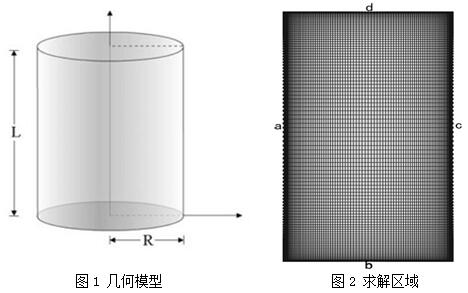
模拟研究用一封闭的圆柱形储粮仓作为研究对象，简化模型见图1和图2。根据实地调查的结果显示，粮仓内部水分含量、温度等参数变化呈现对称分布，并且圆筒仓是轴对称图形，为了节省计算时间，选择圆筒仓轴向截面的一半作为需要模拟计算的几何模型。圆柱底面的直径为（2R）10m，高度（L）10m，x轴方向即为底面半径的方向，y轴为圆柱仓的高度方向。 

1.2 数学模型

1.2.1 控制方程

以小麦作为研究对象，假定小麦为连续介质，因此各守恒方程均适用于本研究中的模拟。小麦的储藏过程中主要涉及到的方程有质量守恒、能量守恒、动量守恒、水分守恒方程。

连续性方程（1）

动量守恒方程（2）

能量守恒方程

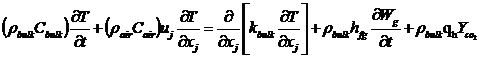（3）

水分守恒方程

（4）

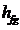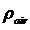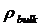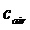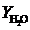其中：基于温度梯度的水蒸气扩散系数；基于水分梯度的水蒸气扩散系数；水蒸气在粮堆中的有效扩散系数；水蒸气扩散系数；σ是定温下水分含量改变引起的分压变化量；是定水分含量下温度改变引起的分压变化量；是空气膨胀系数；粮堆的蒸发潜热；和分别是空气密度和粮堆密度；和分别是空气比热容和粮堆比热容；是粮堆呼吸24h释放的水分；是粮堆呼吸24h的CO₂释放率；是呼吸过程放热量，值为10.738J/mg；是呼吸过程产生的水分量，值为4.09×10^-5kg/mg。

1.2.2 初始条件和边界条件

在模拟过程中，认为边界是无滑移边界，且是不可渗透的。主要研究初始水分14%时的四种情况，分别为初始粮温-10℃时，考虑呼吸热和不考虑呼吸热的两种情况，以及初始粮温30℃时，考虑呼吸热和不考虑呼吸热的两种情况。另外，也研究了初始水分16%时的部分情况，并加以对比分析。

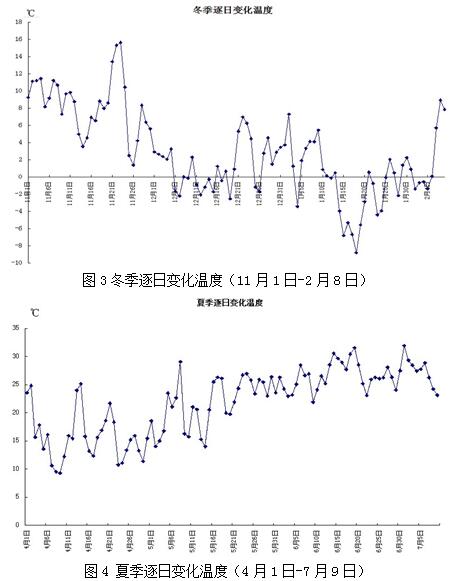
求解区域中边界a是轴对称边界，该边界上热湿通量为零，边界b为地面边界，按绝热条件处理，边界c和d取逐日变化温度（冬季工况取11月1日～2月8日，夏季工况取4月1日～7月9日，数据来源于中国建筑热环境分析专用气象数据集，详见图3、图4）。边界c和d的处理使模拟更加接近于真实情况。

 1.3 数值模拟方法

采用有限元法（finite element method）。即将连续的求解域离散为一系列的单元体，然后在单元体上选取几个点作为节点，然后用控制方程组进行积分处理，得到离散方程组进行计算。有限元法是一种高效常用的计算方法，常用于解决微分方程复杂以及边界条件复杂的数学模型。

2 数学模型验证

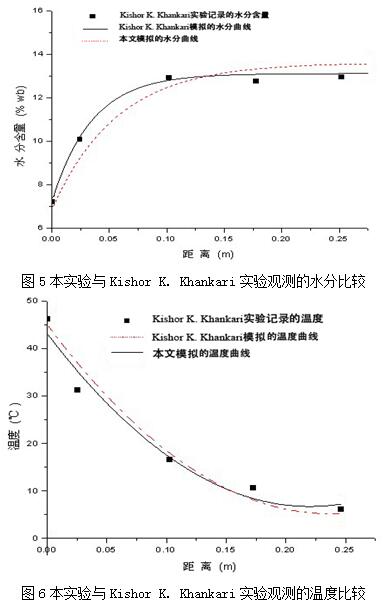
将模拟结果与Kishor K. Khankari的文献中的实验结果做对比，以验证本研究所采用的模型的可靠性， Kishor K. Khankari在自然对流状态下对小麦的水分、温度变化进行了实验研究。

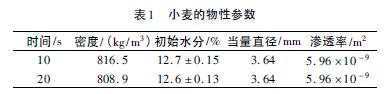
与Kishor K. Khankari的结论进行了温度和水分变化的对比，结果如图5和图6所示。对比分析发现模拟结果与Kishor K. Khankari实验的模拟结果基本吻合，验证了本实验数学模型的有效性。

3 结果与分析

实验模拟了初始粮温为-10℃和30℃的情况，这两种情况分别近似于实际情况中的夏季和冬季工况。每种情况下又分别研究了考虑呼吸热和不考虑呼吸热的情况，以方便进行对比分析。图7~图10列出了初始水分含量为14%的小麦100天后的温度变化和水分变化的情况。

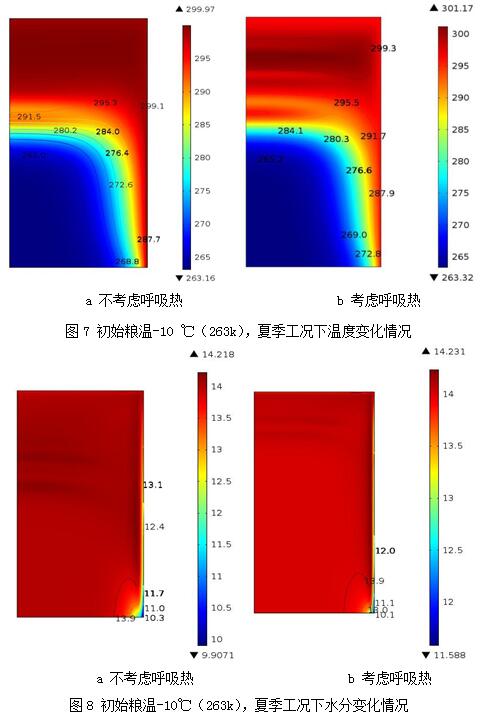
由模拟结果可以发现，当初始粮温为-10℃时（夏季工况），不考虑呼吸作用和考虑呼吸作用两种情况下，100天后粮堆能达到的最高温度均为26℃左右，最低温度在-10℃左右。水分变化的情况也类似，粮堆能达到的最高水分含量时在考虑呼吸和未考虑呼吸时基本相同，最低水分含量考虑呼吸时比不考虑呼吸时大1.5%左右。分析其原因，主要是由于夏季工况时，粮堆的初始温度较低，尽管外界气温逐渐升高，但是由于粮堆导热系数较低，温度升高较慢。这说明当粮食温度较低时，粮堆的呼吸作用对温度的影响较小，对水分含量的影响则稍大一些。

当初始粮温为30℃时（冬季工况），不考虑呼吸作用时，粮堆的最高温度维持在30℃左右，最高水分含量为19.6%，但当考虑呼吸作用时，粮堆的最高温度达到40℃，最高水分含量达到22%，这说明当小麦初始温度较高时，小麦的呼吸作用加强，呼吸作用产生的热量和水分也增加，对粮堆的温度和水分变化的影响比较明显。 

4 结论

基于有限元的方法，利用comsol软件进行模拟，对考虑呼吸作用的储粮仓中小麦的水分含量和温度的变化进行了数值模拟分析，并且模拟过程创新性的选择了变温度的边界条件，使得模拟结果更加贴近于真实情况。通过模拟得到了“非人工干预”条件下近似冬季和夏季温度、水分随时间的变化规律，发现在初始粮温较低时，呼吸作用相对较弱，呼吸作用对粮堆温度和水分的影响较小，初始粮温较高时，呼吸作用旺盛，呼吸作用对粮堆温度和水分的影响十分显著。